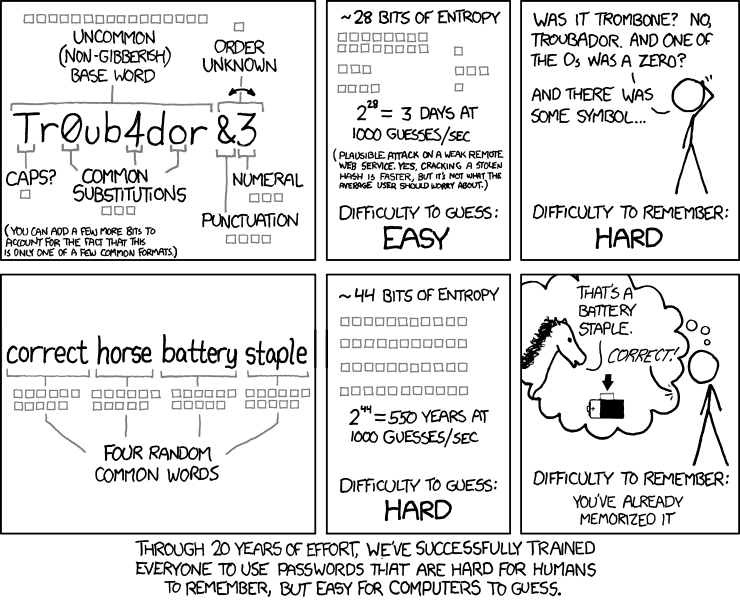
在互联网构建的数字世界中,我们在不同的公共社区、论坛和私人领土都有一个属于自己的数字身份。每个人当然都不愿意身份被盗用或者信息被泄露,但总会有不法之徒试图破坏秩序,造成难以估量的损失。那么,在享受网上冲浪便利的同时,我们有哪些手段可以保障我们的信息安全呢?
前提
本文仅从使用者角度出发,谈论信息泄露的防范措施,但无法杜绝系统本身的安全性问题。不管你的汽车做了多少层措施以减少意外伤害,请不要在危险道路上行驶。信息安全的一个重要前提是,远离脆弱的信息系统。
如果你无法识别系统的安全性,请至少不要在不知名的网站或移动应用中留下你的隐私信息。如果需要进一步核实,这两个网站能够帮到你:Similar Web 和 urlscan。
还有三点老生常谈的事项,在此反复提醒一下:
- 请用正版的操作系统
- 杜绝盗版软件、流氓软件
- 照片共享到社交媒体前移除位置和隐私数据
进一步的,有些危险的行为习惯也需要警惕:
- 远离公共 WiFi 网络,如果一定要用,请用 VPN
- 不要点击陌生的链接(来自短信、邮件或者其他通讯工具)
从黑客角度出发
当我们谈及信息安全的时候,本质上就是防御黑客行为。
而从黑客角度来说,你的头像、ID、快递单号、习惯用语、购买记录、宠物……都会成为泄密的渠道。而本文谈及的安全指南仅限于防范数字生活中的财产损失,而非保护个人隐私问题(其实绝大部分人也不需要做到数字身份的隔离)。
此外,黑客在施展攻击时,并不在意对方账户有多少余额,他们有很多种方式从中牟利。
从一个宏观的角度去思考该问题,畅想一下未来:当下 Web 3.0 的口号越来越响亮,我们拥有的数字资产并不一定只是有形资产的证明,社交、兴趣、信用、虚拟形象这些无形资产也会 token 化。随着数字世界与其承载的资产扩张,其相应的安全产业自然也会随之升级。网络攻防会以令人意想不到的方式随时发生。
让我们回到当下。
当前互联网存在的信息系统依旧普遍采用账号系统做身份认证,保护个人信息安全其实也就是保护账号安全。接下来介绍的工具,能够做到非常简单而有效地保护个人的账号安全。
第一层:密码管理器
你至少需要做到:
- 抛弃简单的或重复的密码
- 拥有一个合格的密码管理器
绝大多数平台在注册时都会提醒你采用高强度的密码,我的建议是:
- 不同平台的密码不要重复,也不要采用同一模式设置
- 不要以大众熟悉的元素或流行文化作为参考
- 不要在密码中添加与自身关联的信息,如纪念日、亲友名称
- 不要仅在首尾添加特殊字符,那样不会让密码更强大
密码管理器是一个让你一劳永逸的软件,它如同一个保险箱,确保你的密码被安全地储存。同时,这类软件通常都是跨平台的,支持自动填充到网站和应用程序中。而你只需要一把钥匙,即「主密码」,解锁该保险箱。
常用的密码管理器有 1Password、LastPass、Bitwarden、Enpass、KeePass 等等,如果需要详细了解和比较这类工具的特性,请访问 AlertnativeTo。
笔者日常使用的是 Bitwarden。Bitwarden 完全免费且开源(支持自行部署服务),支持市面上主流的操作系统和浏览器,也支持保存信用卡、安全问题、TOTP 这类信息。
这里再小小的科普一下 TOTP (Time-based One-Time Password),有时被翻译为安全口令。如果你有用过 Steam 或银行的 USB Key 应该就能明白,其本质是在硬件设备上内置一个生成的「种子」,根据时间变化每隔一定周期更新一次的密码轮。它是一个通用标准协议。只要拿到「种子」,密码管理器就能够帮你计算出当前的 OTP (One-Time Password),就不需要打开特定的应用程序来查看了。
第二层:主密码
当你拥有了一个坚不可摧的保险箱,那么接下来需要做的事情就是,妥善保管箱子的钥匙,即「主密码」。鉴于主密码的重要性,如果主密码泄露或者遗忘,后果简直是灾难性的。
想象一下,也许你去了一个缺少现代技术覆盖的小岛远离尘嚣,拥抱大自然了一两个月,在你惬意地晒着阳光吮吸着 X 牌甜美冰饮的时刻,突然记不得自己的主密码是什么了。这下子真的与世隔绝了,恐怕一时之间慌乱得想回到过去抽当初的自己一巴掌。
为了防止出现这种麻烦事,我们需要一个东西,确保自己的主密码不会被窃取,同时自己也能随时找到它。
有一个算法叫做 Shamir's Secret Sharing (SSS),是密码学中最古老的保密内容共享方案之一。SSS 技术的基础原理是 Lagrange interpolation theorem(拉格朗日插值定理),出自 Adi Shamir(RSA 算法的发明者之一)的论文《How to Share a Secret》。顺便提一下,在 SSS 基础之上增加了校验流程,有一个更强大的构造方案称为 Verifiable Secret Sharing (VSS),是一些共识算法的重要技术。不过保管主密码的话,我们只需要 SSS 就够了。
SSS 的原理形象的解释是这样子的:
全球饮料巨头 X 公司有一口特殊的水源让它长盛不衰,它作为核心商业机密藏在一个巨大的保险库里。现在保险库的密码被转换为 n 个铭牌,按照持有的股份发放给 X 公司的高管,其中集齐了 k(k≤n) 个铭牌后,才能解锁该保险库。如此一来,居心叵测的少数高管无法从中谋取私利,不慎被盗取的一两个铭牌也无法发挥作用。
而具体到数学原理,这里简单介绍一下,是通过构造一个多项式,其中密码被表示为 有限域 。一个典型的有限域例子是用梅森质数 () 做模运算的集合。
想象一下在一个平面中,两点定义一条直线,三点定义一条抛物线,以此类推, 个点定义了一条唯一 次曲线。我们选定了 n 个点,其中每一个点的坐标为 。
那么,在给定的子集 中,用 得到插值,形如公式:
便能得到正确的 。
文末附有 Python 版实现的源代码,如果想直接体验一下,请访问在线版本。如果你日常用 Linux 工作,那么看一看 ssss-split 和 ssss-combine 的手册页吧。
现在,你已经掌握了密码共享的方式。现在你可以分成几个部分,交给信任的亲友,存储到他们的密码管理器中;或者记录到某些隐匿的地方。
主密码,安全 ✅
第三层:2FA 与 SIM 卡 PIN 码
除了账号的密码本身,一些平台会提供双因子验证 (Two-factor authentication, 2FA) 的功能。
总的来说,个人的生理特征(虹膜、指纹)和私人物品(卡片、钥匙)都是一个因子,加上密码构成了双因子。
除了密码,最常用的因子还是我们通常随身携带的手机。手机或邮箱验证码、上文中提到的 OTOP,都是互联网平台典型的 2FA。笔者建议重要的账号能开启 2FA 就开启。
不过国内平台支持 OTOP 的比较少;如果你有国外平台账号的话,建议采用 2FA Authenticator,笔者个人使用的是 Authy,一些大厂出品的如 Google Authenticator 和 Microsoft Authenticator 也都值得信赖。
详细说一下国内的情况,短信验证本质上是验证 SIM 卡。我们要确保 SIM 卡丢失或被恶意拷贝的时候验证一次。
SIM 卡可以设置 PIN (Personal Identification Number) 码,如果你用 iPhone 的话,参考这篇官方文档完成设置。顺便一提,如果遗忘了 PIN 码,需要拿 PUK (Personal Identification Number Unlock Key) 码去运营商那里解锁 PIN 码,如果多次猜测错误,就会永久性锁卡(就只能更换 SIM 卡了)。
最后,记得给手机设置上六位以上的密码。
让我们开始网上冲浪吧!
参考资料
"""
The following Python implementation of Shamir's Secret Sharing is
released into the Public Domain under the terms of CC0 and OWFa:
https://creativecommons.org/publicdomain/zero/1.0/
http://www.openwebfoundation.org/legal/the-owf-1-0-agreements/owfa-1-0
See the bottom few lines for usage. Tested on Python 2 and 3.
"""
from __future__ import division
from __future__ import print_function
import random
import functools
# 12th Mersenne Prime
# (for this application we want a known prime number as close as
# possible to our security level; e.g. desired security level of 128
# bits -- too large and all the ciphertext is large; too small and
# security is compromised)
_PRIME = 2 ** 127 - 1
# 13th Mersenne Prime is 2**521 - 1
_RINT = functools.partial(random.SystemRandom().randint, 0)
def _eval_at(poly, x, prime):
"""Evaluates polynomial (coefficient tuple) at x, used to generate a
shamir pool in make_random_shares below.
"""
accum = 0
for coeff in reversed(poly):
accum *= x
accum += coeff
accum %= prime
return accum
def make_random_shares(secret, minimum, shares, prime=_PRIME):
"""
Generates a random shamir pool for a given secret, returns share points.
"""
if minimum > shares:
raise ValueError("Pool secret would be irrecoverable.")
poly = [secret] + [_RINT(prime - 1) for i in range(minimum - 1)]
points = [(i, _eval_at(poly, i, prime))
for i in range(1, shares + 1)]
return points
def _extended_gcd(a, b):
"""
Division in integers modulus p means finding the inverse of the
denominator modulo p and then multiplying the numerator by this
inverse (Note: inverse of A is B such that A*B % p == 1) this can
be computed via extended Euclidean algorithm
http://en.wikipedia.org/wiki/Modular_multiplicative_inverse#Computation
"""
x = 0
last_x = 1
y = 1
last_y = 0
while b != 0:
quot = a // b
a, b = b, a % b
x, last_x = last_x - quot * x, x
y, last_y = last_y - quot * y, y
return last_x, last_y
def _divmod(num, den, p):
"""Compute num / den modulo prime p
To explain what this means, the return value will be such that
the following is true: den * _divmod(num, den, p) % p == num
"""
inv, _ = _extended_gcd(den, p)
return num * inv
def _lagrange_interpolate(x, x_s, y_s, p):
"""
Find the y-value for the given x, given n (x, y) points;
k points will define a polynomial of up to kth order.
"""
k = len(x_s)
assert k == len(set(x_s)), "points must be distinct"
def PI(vals): # upper-case PI -- product of inputs
accum = 1
for v in vals:
accum *= v
return accum
nums = [] # avoid inexact division
dens = []
for i in range(k):
others = list(x_s)
cur = others.pop(i)
nums.append(PI(x - o for o in others))
dens.append(PI(cur - o for o in others))
den = PI(dens)
num = sum([_divmod(nums[i] * den * y_s[i] % p, dens[i], p)
for i in range(k)])
return (_divmod(num, den, p) + p) % p
def recover_secret(shares, prime=_PRIME):
"""
Recover the secret from share points
(x, y points on the polynomial).
"""
if len(shares) < 3:
raise ValueError("need at least three shares")
x_s, y_s = zip(*shares)
return _lagrange_interpolate(0, x_s, y_s, prime)
def main():
"""Main function"""
secret = 1234
shares = make_random_shares(secret, minimum=3, shares=6)
print('Secret: ',
secret)
print('Shares:')
if shares:
for share in shares:
print(' ', share)
print('Secret recovered from minimum subset of shares: ',
recover_secret(shares[:3]))
print('Secret recovered from a different minimum subset of shares: ',
recover_secret(shares[-3:]))
if __name__ == '__main__':
main()